Bayesian Ridge Regression¶
Computes a Bayesian Ridge Regression on a synthetic dataset
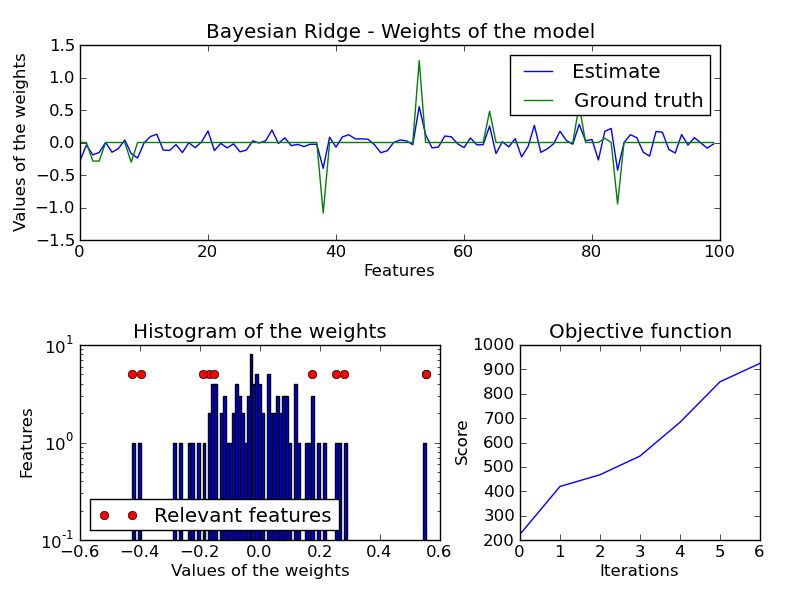
Python source code: plot_bayesian_ridge.py
print __doc__
import numpy as np
import pylab as pl
from scipy import stats
from scikits.learn.linear_model import BayesianRidge
################################################################################
# Generating simulated data with Gaussian weigthts
np.random.seed(0)
n_samples, n_features = 50, 100
X = np.random.randn(n_samples, n_features) # Create gaussian data
# Create weigts with a precision lambda_ of 4.
lambda_ = 4.
w = np.zeros(n_features)
# Only keep 10 weights of interest
relevant_features = np.random.randint(0, n_features, 10)
for i in relevant_features:
w[i] = stats.norm.rvs(loc = 0, scale = 1./np.sqrt(lambda_))
# Create noite with a precision alpha of 50.
alpha_ = 50.
noise = stats.norm.rvs(loc = 0, scale = 1./np.sqrt(alpha_), size = n_samples)
# Create the target
y = np.dot(X, w) + noise
################################################################################
# Fit the Bayesian Ridge Regression
clf = BayesianRidge(compute_score=True)
clf.fit(X, y)
################################################################################
# Plot true weights, estimated weights and histogram of the weights
pl.figure()
axe = pl.axes([0.1,0.6,0.8,0.325])
axe.set_title("Bayesian Ridge - Weights of the model")
axe.plot(clf.coef_, 'b-', label="Estimate")
axe.plot(w, 'g-', label="Ground truth")
axe.set_xlabel("Features")
axe.set_ylabel("Values of the weights")
axe.legend(loc="upper right")
axe = pl.axes([0.1,0.1,0.45,0.325])
axe.set_title("Histogram of the weights")
axe.hist(clf.coef_, bins=n_features, log=True)
axe.plot(clf.coef_[relevant_features],5*np.ones(len(relevant_features)),'ro',
label="Relevant features")
axe.set_ylabel("Features")
axe.set_xlabel("Values of the weights")
axe.legend(loc="lower left")
axe = pl.axes([0.65,0.1,0.3,0.325])
axe.set_title("Objective function")
axe.plot(clf.scores_)
axe.set_ylabel("Score")
axe.set_xlabel("Iterations")
pl.show()
