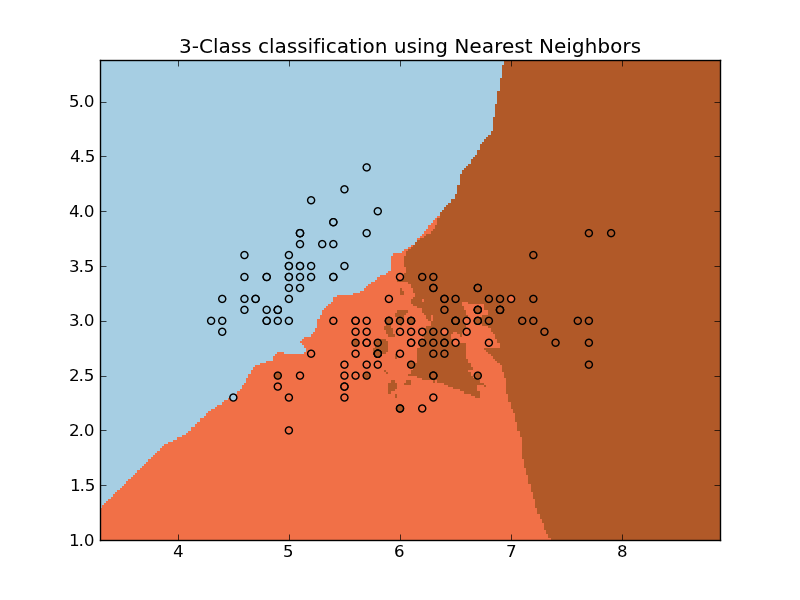
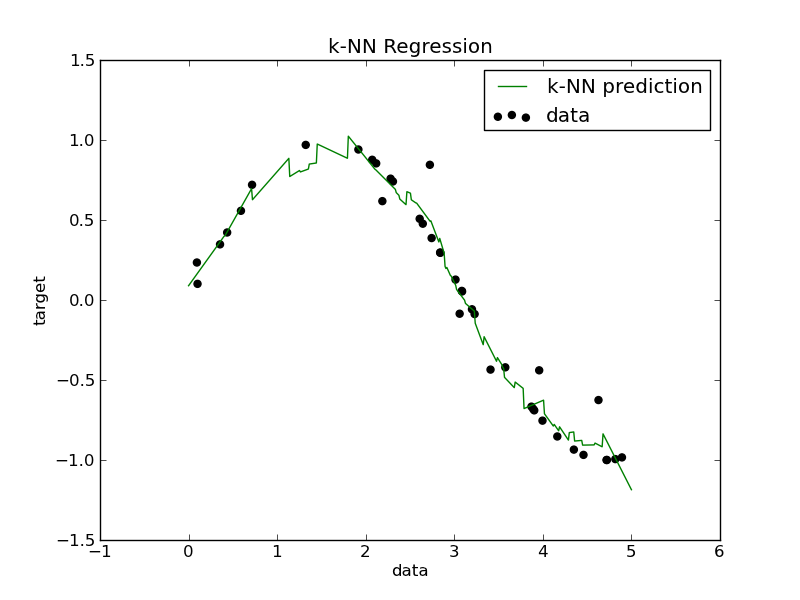
3.4. Nearest Neighbors

The principle behind nearest neighbor methods is to find the k training points closest in euclidean distance to x0, and then classify using a majority vote among the k neighbors.

Despite its simplicity, nearest neighbors has been successful in a large number of classification problems, including handwritten digits or satellite image scenes. It is ofter successful in situation where the decision boundary is very irregular.

3.4.1. Classification

The Neighbors estimators implements the nearest-neighbors classification method using a vote heuristic: the class most present in the k nearest neighbors of a point is assigned to this point.

Examples:

• Nearest Neighbors: an example of classification using nearest neighbor.

3.4.2. Regression

The NeighborsBarycenter estimator implements a nearest-neighbors regression method using barycenter weighting of the targets of the k-neighbors.

Examples:

• k-Nearest Neighbors regression: an example of regression using nearest neighbor.

3.4.3. Efficient implementation: the ball tree

Behind the scenes, nearest neighbor search is done by the object BallTree, which is a fast way to perform neighbor searches in data sets of very high dimensionality.

This class provides an interface to an optimized BallTree implementation to rapidly look up the nearest neighbors of any point. Ball Trees are particularly useful for very high-dimensionality data, where more traditional tree searches (e.g. KD-Trees) perform poorly.

The cost is a slightly longer construction time, though for repeated queries, this added construction time quickly becomes insignificant.

A Ball Tree reduces the number of candidate points for a neighbor search through use of the triangle inequality:

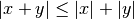
Each node of the BallTree defines a centroid, C, and a radius r such that each point in the node lies within the hyper-sphere of radius r, centered at C. With this setup, a single distance calculation between a test point and the centroid is sufficient to determine a lower bound on the distance to all points within the node. Carefully taking advantage of this property leads to determining neighbors in O[log(N)] time, as opposed to O[N] time for a brute-force search.

A pure C implementation of brute-force search is also provided in function knn_brute().

References:

• “Five balltree construction algorithms”, Omohundro, S.M., International Computer Science Institute Technical Report