A demo of the mean-shift clustering algorithm

Reference: K. Funkunaga and L.D. Hosteler, “The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition”

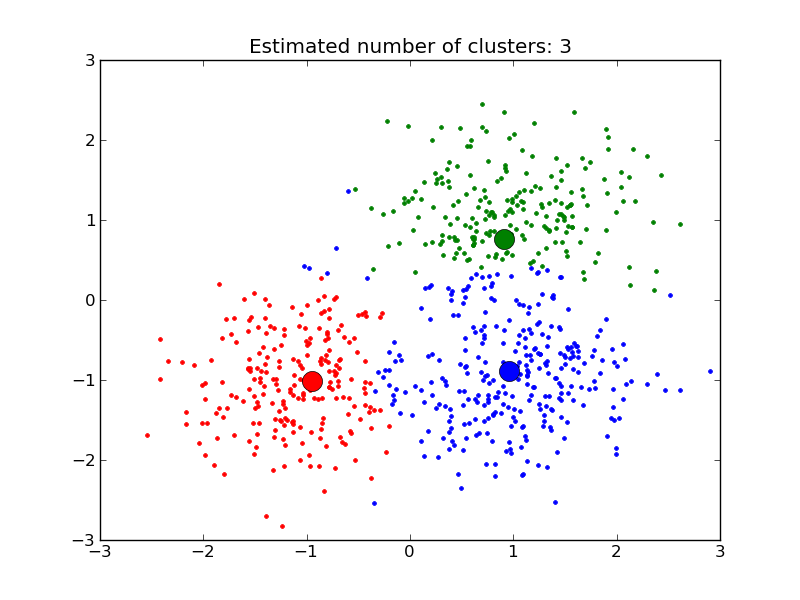
Python source code: plot_mean_shift.py

import numpy as np
from scikits.learn.cluster import MeanShift, estimate_bandwidth

################################################################################
# Generate sample data
np.random.seed(0)

n_points_per_cluster = 250
n_clusters = 3
n_points = n_points_per_cluster*n_clusters
means = np.array([[1,1],[-1,-1],[1,-1]])
std = .6
clustMed = []

X = np.empty((0, 2))
for i in range(n_clusters):
    X = np.r_[X, means[i] + std * np.random.randn(n_points_per_cluster, 2)]

################################################################################
# Compute clustering with MeanShift
bandwidth = estimate_bandwidth(X, quantile=0.3)
ms = MeanShift(bandwidth=bandwidth)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_

labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)

print "number of estimated clusters : %d" % n_clusters_

################################################################################
# Plot result
import pylab as pl
from itertools import cycle

pl.figure(1)
pl.clf()

colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
    my_members = labels == k
    cluster_center = cluster_centers[k]
    pl.plot(X[my_members,0], X[my_members,1], col+'.')
    pl.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
                                    markeredgecolor='k', markersize=14)
pl.title('Estimated number of clusters: %d' % n_clusters_)
pl.show()